POS成像仿真

1 摘要测试

任务目标与程序功能：对POS的光路进行仿真，验证POS技术的可行性，并优化光路的设计参数选择，从而实现最优的测试效果。

要应用POS技术，关键在于掩模版的设计与光路的搭建。本程序首先对POS光路进行建模研究，通过对光场进行离散化描述，编写光场传输函数求解菲涅尔衍射，仿真计算光场通过掩模版的衍射情况，最终输出不同光路参数与掩膜版设置下在成像靶面显示的图像，并依据仿真结果进行了波前重构的解算，验证了POS技术的可行性。

2 问题背景

POS技术的背景与基本原理

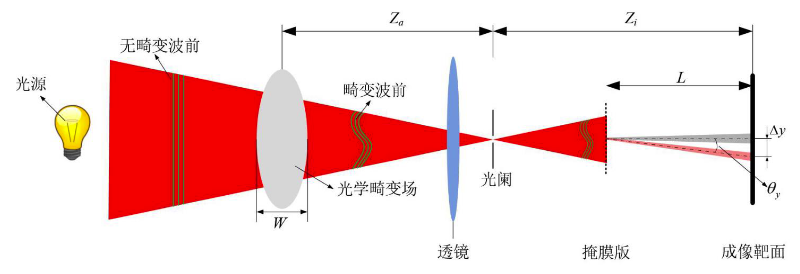
光掩膜导向纹影(Photomask Oriented Schlieren,POS)技术将随机分布二元掩膜版集成进相机成像光路内部，替代了应用背景纹影 (Background Oriented Schlieren,BOS)技术所需的大面积预设背景，实现方便集成的大视场高精度流场测量。

图 1 POS原理光路

如图1所示，具有无畸变波前的光线在穿过光学畸变场之后会出现比较明显的波前畸变。在经过等效镜头组后穿过包含有大量微型通光孔的掩膜版后，变成大量的光束照射到成像靶面上，形成类似图2所示的光斑图像。考虑到普通镜头成像特点，成像靶面上接收的光斑尺寸会比对应通光孔孔径要大，变化量可以通过简单的几何关系粗略计算得到。

图 2 两种掩膜版图案

图1中掩膜版与成像靶面间的灰色细光束代表了无光学畸变场的光线穿过某个通光孔后形成的光束，相对应的红色细光束是有光学畸变场时光线穿过对应通光孔后形成的，而完整光场将会形成与图2类似的光斑图像。将畸变前后的光斑图像进行比较，可以对光学畸变场实现测量。

为了实现较高的相位分辨率，需要尽可能增大掩模版投影像距，即图1中的掩模版与成像靶面间的距离；同时为了实现较高的空间分辨率，还应尽可能增大掩模版开孔线度。以上两种因素均会放大掩模版开孔的衍射现象，换言之，POS技术的相位分辨率与空间分辨率均受到掩模版衍射物理极限的制约。因此，要需要通过优化设计掩模版开孔方式与光路参数，针对不同的波前测试需求，平衡相位分辨率与空间分辨率，以期实现最优测试效果。

本文旨在通过数值仿真的方式对POS技术中掩模版的衍射现象进行分析，并依照仿真结果对POS光路参数的选择与掩模版加工方式进行针对性优化设计，以降低设计周期与实验成本。

3 仿真原理

介绍本程序进行衍射仿真计算的理论基础

3.1 基尔霍夫公式

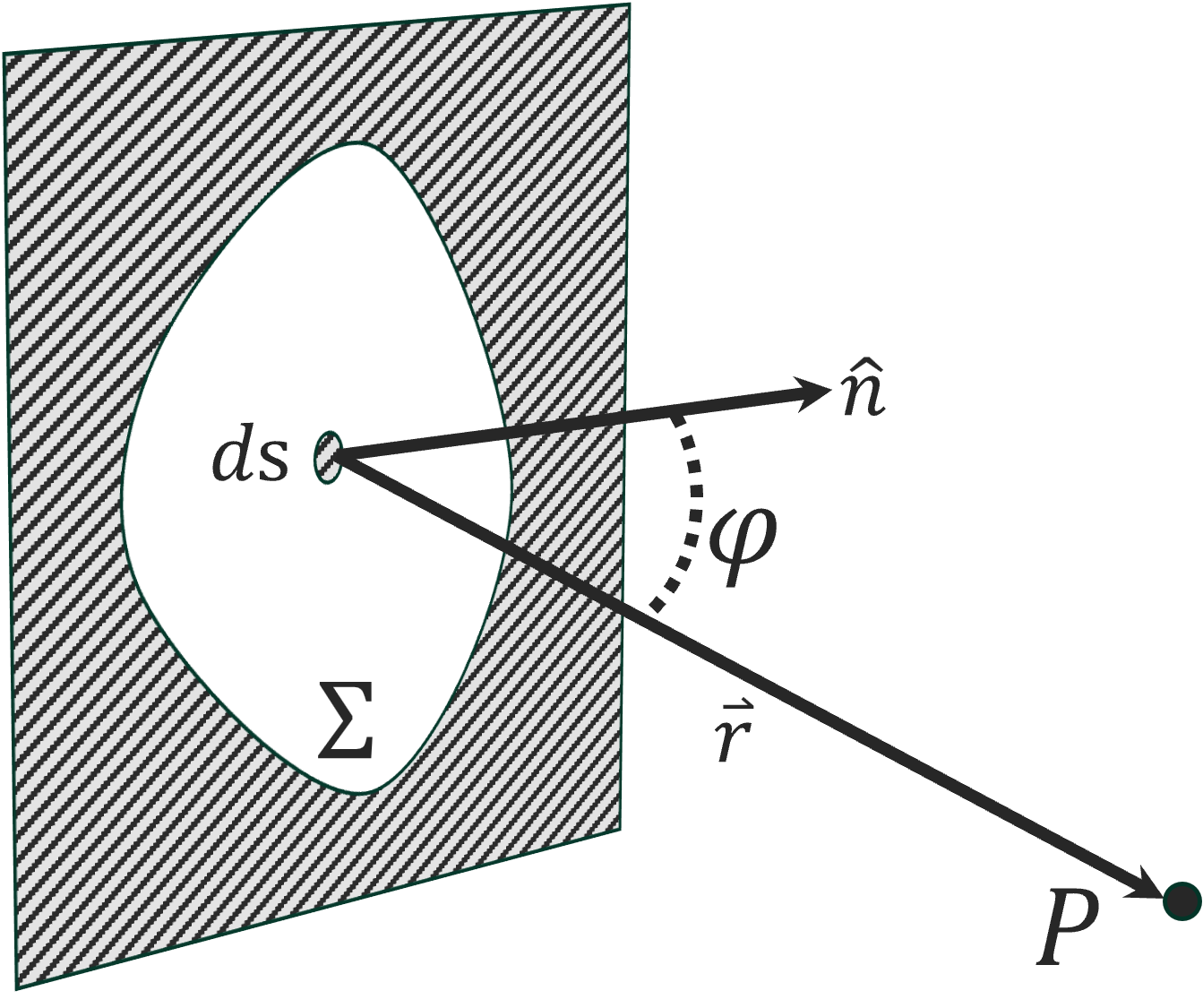
图 3 波阵面示意图	图 4 倾斜因子示意图

根据惠更斯-菲涅尔原理(Huygens–Fresnel principle)，如图3所示的空间中一点的振动等于衍射孔面上所有的子波源所引发振动的相干叠加，子波源引发振动的振幅与面元为正比关系。

点振动的振幅为整个面上子波源引发振动的叠加，积分表达式为^[1]

上式被称为菲涅尔衍射积分公式(Fresnel Diffractive Integral)。式中，为面上的光场分布，是面元与场点的距离，与分别为光波圆频率与波长；是个特定的比例系数，为倾斜因子表征由面元引发的次波并非各向同性，但均没有给出具体的定义。

基尔霍夫基于麦克斯韦理论，推导得出比例系数与倾斜因子，代入式(1)整理后，得到用于定量求解衍射积分的基尔霍夫衍射公式(Kirchoff's Diffraction Formula)为^[2]

式中，, 、分别为如图4所示的面元法向量与照明光波矢、出射光波矢的夹角。

3.2 菲涅尔衍射

图 5 两坐标系定义图

如图5所示建立直角坐标系，用平面描述衍射屏，平面描述接收屏，可以将写为^[1:1]

菲涅尔衍射是一种近似情况，当时，在傍轴条件下再取倾斜因子，(2)式变成

也可写为

3.3 利用傅立叶变换计算菲涅尔衍射

用表示傅立叶变换，用表示与的卷积，由傅立叶变换的卷积性质，有

对照式(4)，可将菲涅尔衍射的积分式写为

4 计算模型

介绍本程序对问题的抽象与假设

进行衍射传播计算比较消耗计算资源，因此在现阶段对纳入仿真的光路进行简化，仅针对光场通过掩模版这一核心问题进行仿真计算。掩膜版由随机分布的通光开孔组成，每一个通光孔可以作为一个衍射基元，将这些衍射基元在成像靶面的衍射场相干叠加，即可获得最终的成像结果。

4.1 衍射基元计算模型

本模型针对每个衍射基元进行分析，假设POS光路的入射光场为叠加了小相位畸变的单色平面波前，经过定焦镜头与等效光阑，最终传播至掩模版。若镜头组的传递函数可解析得出，抑或是通过镜头组后的光场已经通过仿真得出，则掩模版的照明光波前可以被确认下来。

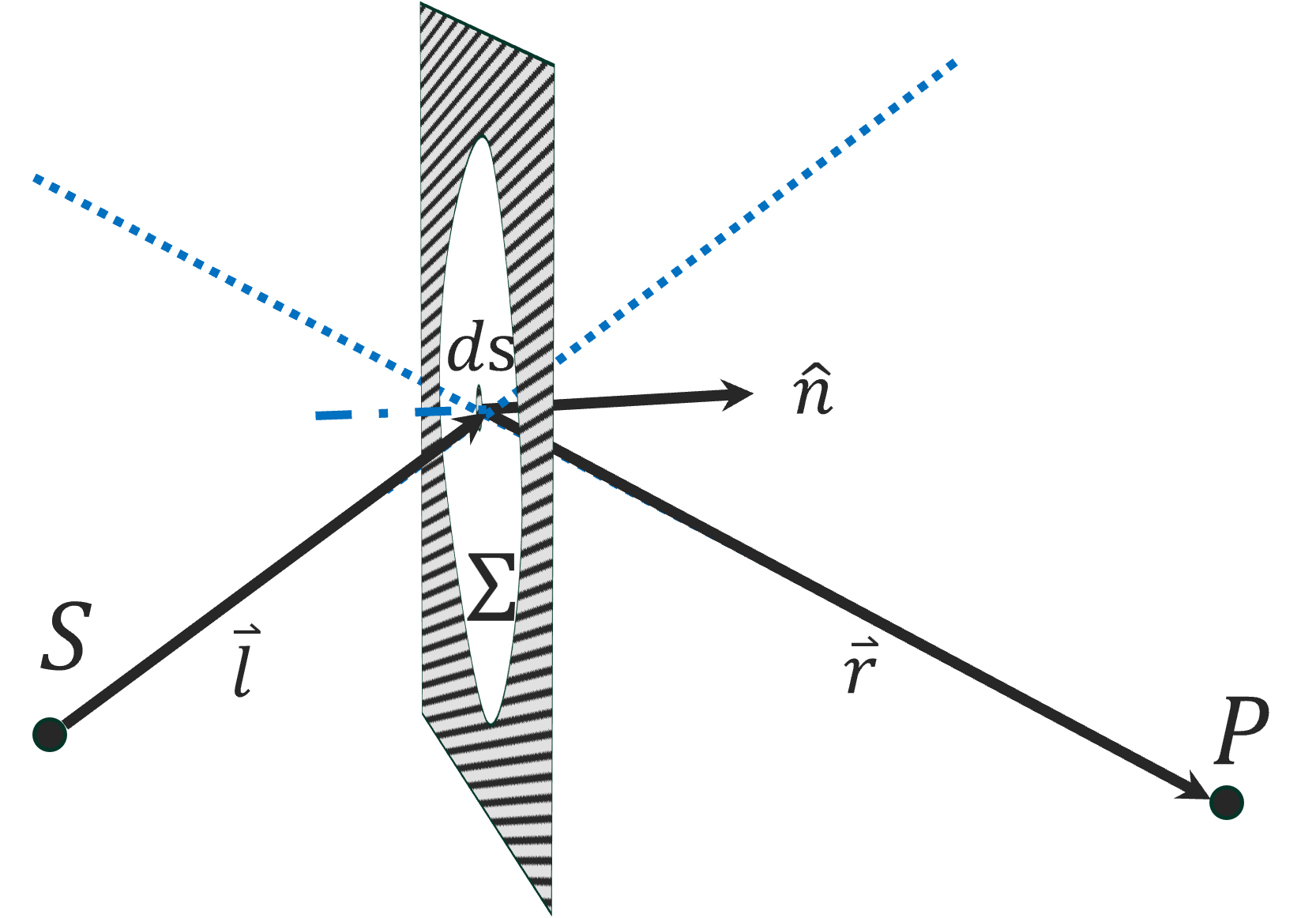
图 6 衍射系统示意图

对于如图6所示的照明光、掩膜版与成像靶面三者构成的衍射系统，具有考量意义的是三个波前，分别是：掩膜版前侧的照明波前，即入射场；经过掩膜版作用的衍射波前，即透射场；传播到达成像靶面的成像波前，即接收场。^[2:1]整个衍射问题的计算可被分为两个步骤，一是解入射场经过掩膜版作用变为透射场的透射问题，二是解透射场经过空间传播变为接收场的传播问题。

对于本问题中，典型值为：衍射距离，掩膜版开孔线度，可以满足菲涅尔近似，则传播问题可由式(7)计算得出。而透射问题可由屏函数描述：

式(8)意为，对于一个衍射屏可以定义一个屏函数，透射波前就等于入射波前乘上这个屏函数。

对于我们关心的掩膜版而言，其屏函数为

4.2 分解叠加模型

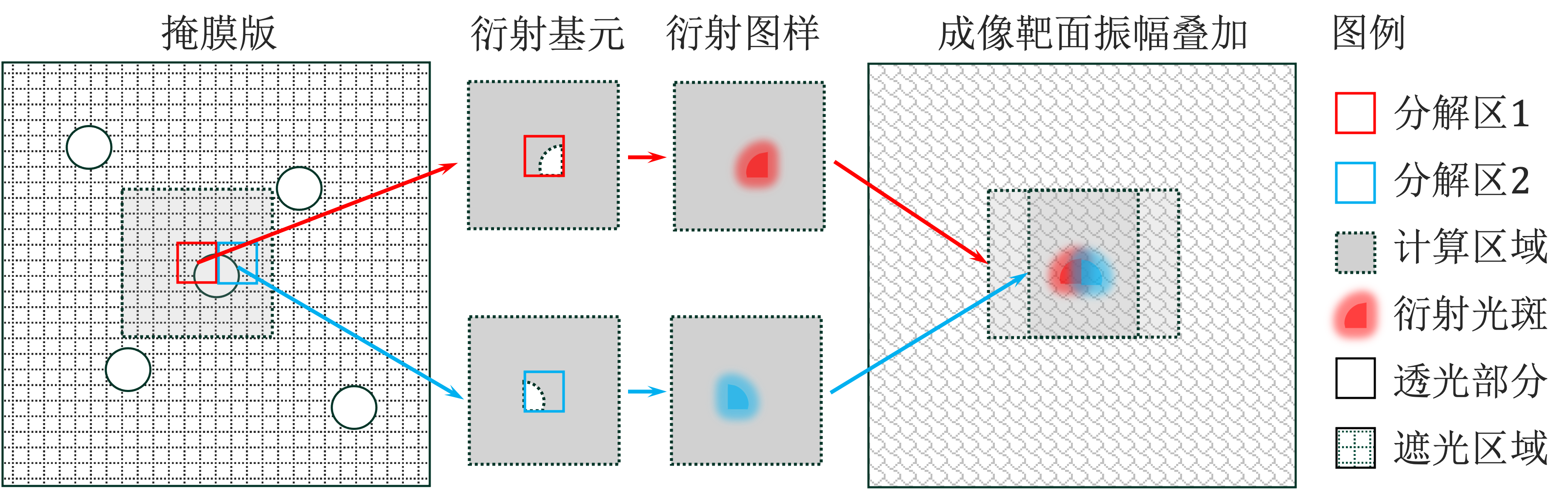
图 7 分解叠加模型

如果直接求解整个掩膜版的衍射现象，即使利用卷积算法或快速傅立叶变换(Fast Fourier Transform,FFT)算法，也将会产生很大的计算量，而且考虑到掩膜版尺寸与衍射距离处于同一数量级，菲涅尔近似也随之失效。

因此，本程序在计算时提出如图7所示的分解叠加模型，将掩膜版划分为若干个小的分解区，将分解区内的透光区域置于计算区域，来分别求解菲涅尔衍射，最后将计算区域得出的衍射场的相干叠加，从而求得总衍射场。

理论上讲，如果计算区域选取得充分大，则叠加结果将与直接计算的结果将足够接近，但这也将带来更大的计算量，并无实践意义。而在实际情况下，由于倾斜因子的影响，远离光轴区域的振幅矢量趋近于零，再加之掩膜版开孔随机分布的影响，我们可以近似地将计算区域外远离光轴场点的振幅假设为零，故可以将计算区域取的稍小一些，来减小计算量。

5 代码实现

关于代码细节的一些说明

5.1 光场离散化

现代光学中，“波前”的概念已经由等相面扩展为光场中的任意曲面，一般是指某一个平面。而波前函数可以描述波前上的复振幅分布，包含了振幅分布与位相分布信息，再知道光波长，就可以描述出单色定态波场的光场。

图 8 光场离散化计算

如图8所示，为将研究平面上的波前离散化，选取、方向上合适的分划数，由研究平面的尺寸可算得每个离散网格的位置信息，并建立一个复矩阵存储振幅信息、、，就可以离散化描述出光场信息。依据此方法，可分别描述入射场、透射场、接收场以及作为透射屏的掩膜版屏函数。

5.2 掩膜版散斑生成

掩膜版通光孔的设置是影响到POS技术测试性能的关键因素。随机分布的通光孔可以被视为散斑图像，散斑图像将直接影响到成像靶面光斑分布情况。散斑的选取要考虑到的因素有很多，如为了匹配CCD靶面进光量而调节散斑密排度、抑制衍射现象影响而调节通光孔开孔线度与形状、提升后期匹配算法收敛速度而调整偏移量与随机性等。因此，要综合考虑多种因素，选择合适的散斑生成算法生成屏函数。

5.3 光场传播函数

利用式(2)，已知一个空间中一个波前，便可通过数值积分仿真得出下一平面的波前分布，但其运算量过大，运行效率较低。

衍射模型符合菲涅尔近似，则式(2)可近似由式(7)替代，利用卷积算法或FFT算法，可以大幅度提高计算效率。

但值得注意的是，若选用FFT算法，还应考虑到，由于傅立叶变换本来是对衍射屏平面的无穷积分，因此将计算区域的尺寸取得越大结果越准确，可以滤去离散化FFT计算所引入的远离轴心区域的高频分量导致的计算误差。而在计算区域内进行离散化时，也要选取足够的分划数，来满足二次相位因子函数的理想采样间隔要求以及光场本身采样间隔要求。

6 仿真结果

6.1 模型假设验证

6.1.1 验证衍射基元计算模型

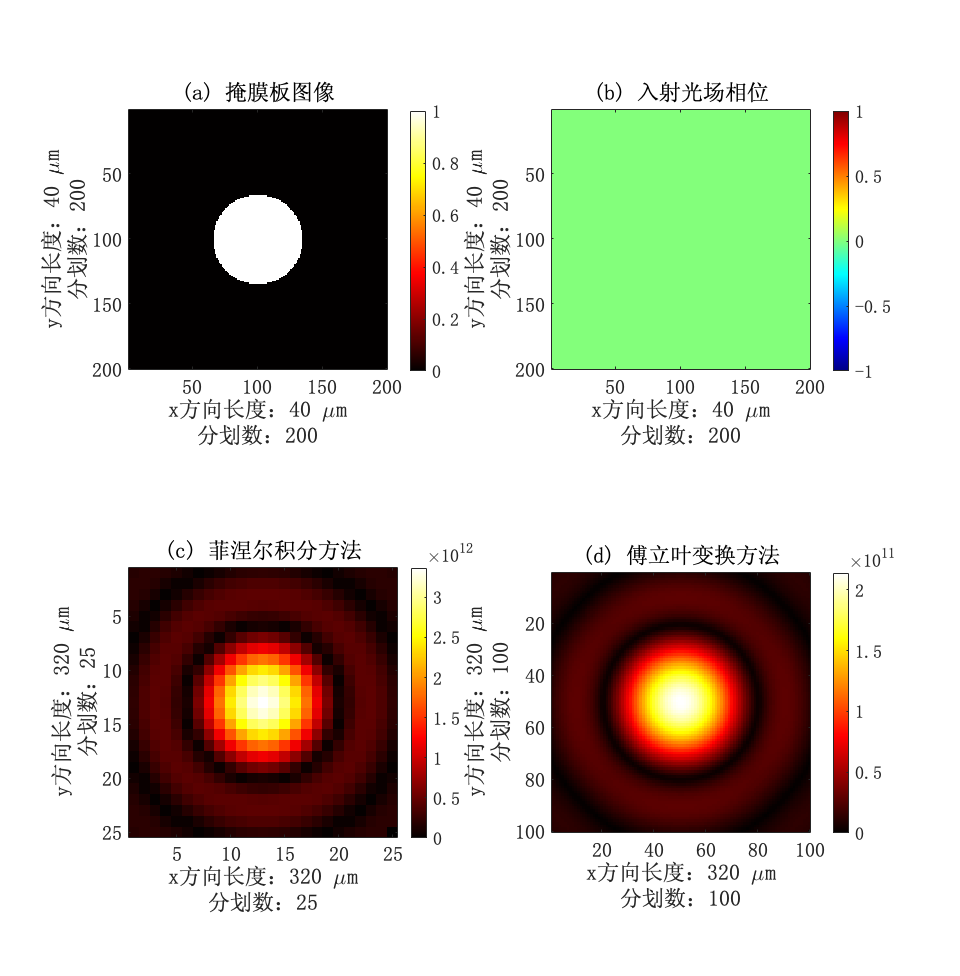
先取最简单的情况，验证衍射基元计算模型仿真的有效性。取衍射基元为圆形通光孔，照明波前为平面波，分别采用式(5)菲涅尔积分与式(7)FFT算法求解衍射问题，结果如下。

图 9 圆孔衍射结果

取开孔半径，平面波前垂直入射，衍射屏尺寸，结果如图9所示，可以见得，FFT方法与菲涅尔积分方法得出的衍射图样一致。

	图 10 减小衍射距离

取开孔半径，平面波前垂直入射，衍射屏尺寸，逐渐减小衍射距离，计算结果如图10所示，可以发现，随着衍射距离的减小，衍射光斑也随之缩小。

	图 11 扩大圆孔直径

同样的，为了抑制衍射效应，还可以扩大通光圆孔的直径，取衍射距离，平面波前垂直入射，衍射屏尺寸与衍射屏一致为，开孔半径分别为、与，计算结果如图11所示。可以发现，随着开孔半径的扩大，虽然衍射效应减弱，但投影面积也随之增大，因此，需要折中选取一个合适的开孔半径。

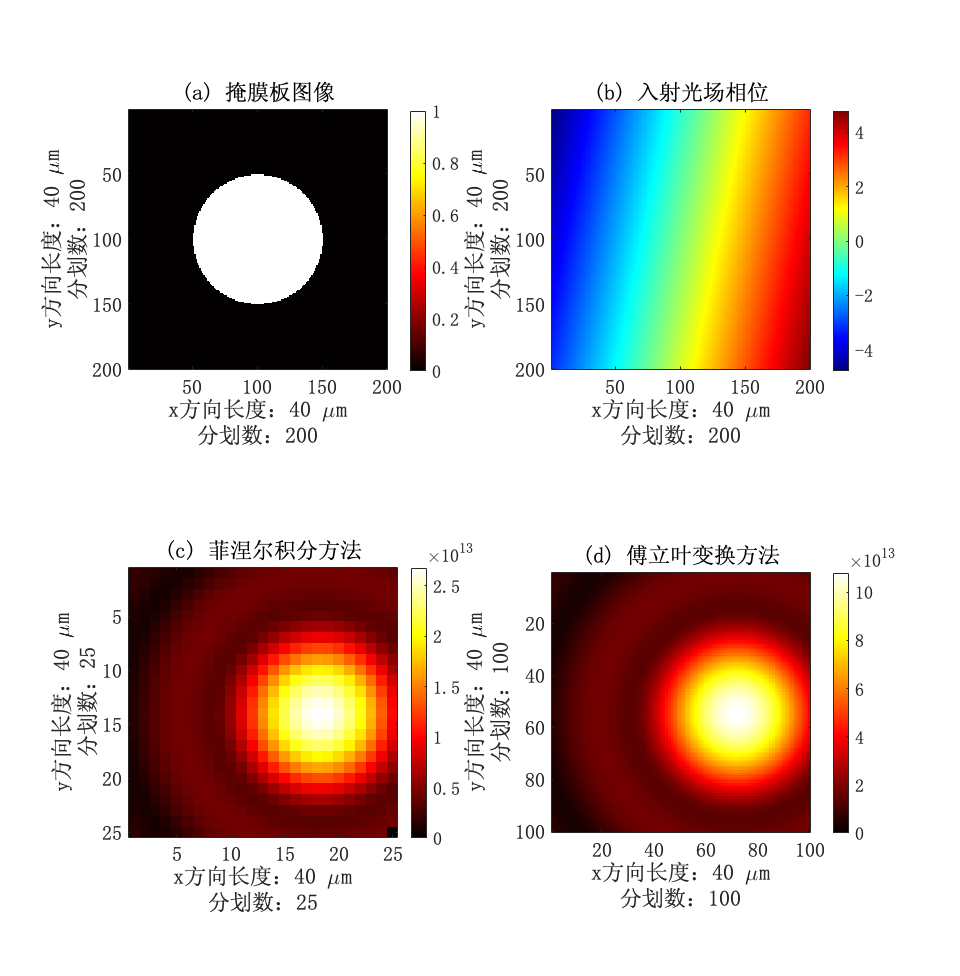
图 12 平面波前斜入射

图12则是平面光斜入射结果，取开孔半径，衍射距离，衍射屏尺寸为，平面波前入射角度为、，可见在小角度下，光斑变形不大，而衍射光斑也随之偏移，偏移量可由简单几何关系预知。

6.1.2 验证分解叠加模型

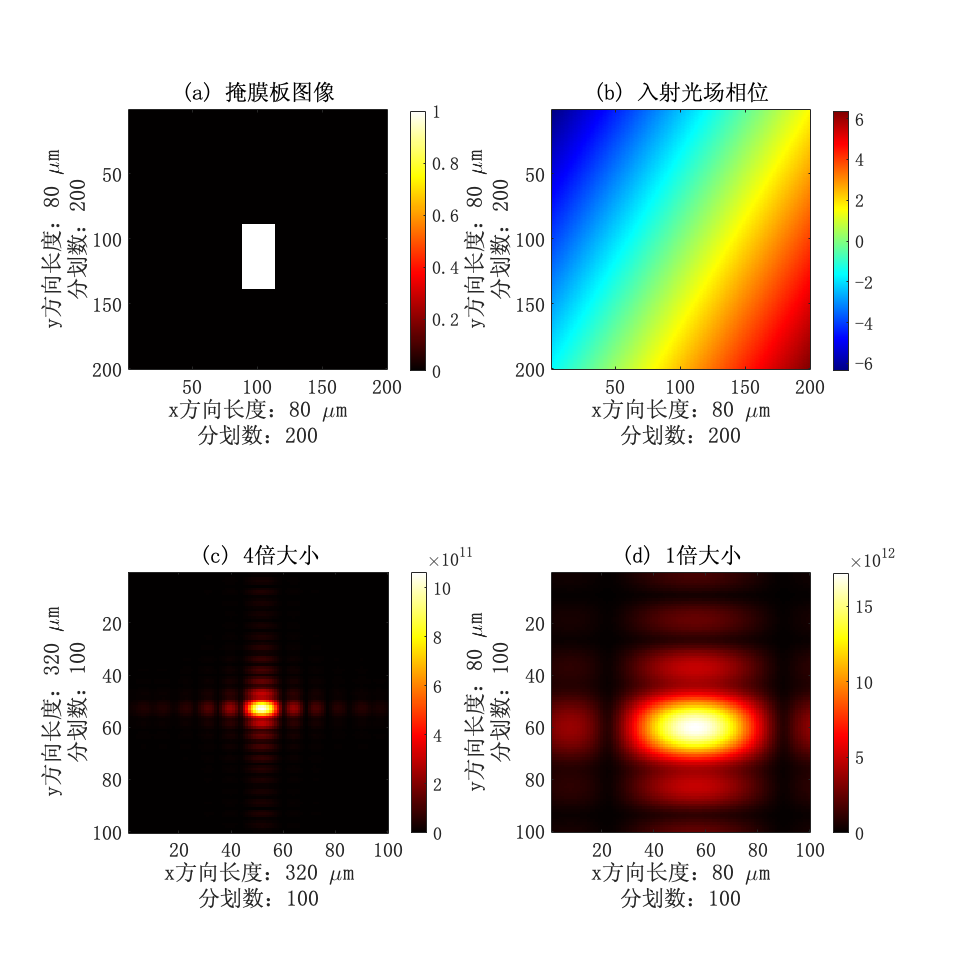
分解叠加模型假设下，合衍射场可由所有分解区计算得出的分衍射场相干叠加得出，取如图13所示的最简单的矩形通光孔的情形进行验证。

图 13 分解叠加模型验证示意

本算例将掩膜版开孔取为长宽的矩形，则如图13所示其两分解区域的开孔为的矩形。计算衍射距离，衍射屏尺寸为，平面波前入射角度为、时，整体计算结果如图14所示。

图 14 分解叠加模型验证

分别计算两个分解衍射场，并将其分别按照振幅矢量相干叠加与绝对光强线性叠加，结果如图15所示。

	图 15	分解叠加模型

可见，图15(c)所示的相干叠加结果与图14(d)所示的直接计算结果一致，但是，图15(d)的光强线性叠加结果与图14(d)具有较大差异，因此，在利用分解叠加模型计算时，需要选取一个比分解区大若干倍大计算区域。

	图 16	相距较远的圆孔

而当计算区域选取得足够大，两个开孔距离足够远时时，相干叠加与线性相加的结果差异将会减小，如图16(a)，取两个半径、圆心相距的圆形开孔，在衍射距离，衍射屏尺寸为，平面波垂直入射时直接算得其合衍射场如16(b)所示，利用分解叠加模型分别计算其两个开孔的分解衍射场，相干叠加与线性相加的结果分别如图16(c)、(d) 所示。可以看出，图16(b)、(c)、(d)三种不同计算方式计算结果差异不大，因此，在选取合适的计算参数的情况下，分解叠加模型不会丢失衍射场用于后续进行波前重构的主要信息。

6.2 仿真计算结果

由于算力有限，目前只选取了实际掩膜版尺寸的十分之一进行试算，对比可知，取马赛克式的掩膜版能够使波前重构算法更好的收敛（真的吗？需要后续实验验证），取基元为的矩形开孔，生成尺寸、分划数的掩膜版，在尺寸、分划数的成像靶面上进行仿真，分别采用平面波前与球面汇聚波前作为参考波前与畸变波前入射，衍射距离，仿真结果如图17所示。（这幅图忘记保存fig文件了，重算还没算完，所以图片注释文本看不清）

图 17 试算结果

6.3 波前重构结果

针对图17给出的结果，陶能武初步波前重构的结果，如图18所示。

图 18 试算结果的波前重构结果

7 改进方向

7.1 待给出的定量结果

1. 优化得出最佳开孔线度：随着通光孔开孔直径的增大，衍射效应减弱可以使光斑变小，与此同时投影面积增大会导致光斑直径变大，可以编写一个光斑识别函数，来确定可分辨的光斑直径，优化出一个合理的开孔直径，结果预计将与衍射距离、光斑识别判据相关。
2. 如何选取合适的计算区域：需要使用一个比较小的试算掩膜版，计算出掩膜版相聚最远的边上对另一边上光强的影响，看什么距离上这些影响不可忽落，影响到衍射图样形状。

7.2 几个优化思路待验证

1. 采样频率该如何确定：崔文乐, 韩利琪, 霍晓敏, 杨丽君和张素恒. 《菲涅尔衍射积分的单次傅里叶变换算法》. 大学物理, 2019年.
2. 大尺寸卷积如何优化cache：《GPU图像处理的FFT和卷积算法及性能分析-【维普期刊官网】- 中文期刊服务平台》. 见于 2022年9月10日.

7.3 没什么思路

1. 为何要取马赛克式掩膜版，需要仿真结果支撑：如何设计算例能够支撑这个结论呢？

---

1. 钱晓凡, 胡涛和张晔. 《基于MATLAB的衍射场模拟计算》. 昆明理工大学学报：理工版 29, 期 3 (2004年): 132–34. ↩︎ ↩︎

2. 钟锡华. 《傅里叶变换光学基本原理讲座》. 物理, 傅里叶变换光学基本原理讲座, 11, 期 8 (1982年). ↩︎ ↩︎