01_POS原理:成像仿真
摘要
任务目标与程序功能:对POS的光路进行仿真,验证POS技术的可行性,并优化光路的设计参数选择,从而实现最优的测试效果。
要应用POS技术,关键在于掩模版的设计与光路的搭建。本程序首先对POS光路进行建模研究,通过对光场进行离散化描述,编写光场传输函数求解菲涅尔衍射,仿真计算光场通过掩模版的衍射情况,最终输出不同光路参数与掩膜版设置下在成像靶面显示的图像,并依据仿真结果进行了波前重构的解算,验证了POS技术的可行性。
问题背景
POS技术的背景与基本原理
光掩膜导向纹影(Photomask Oriented Schlieren,POS)技术将随机分布二元掩膜版集成进相机成像光路内部,替代了应用背景纹影 (Background Oriented Schlieren,BOS)技术所需的大面积预设背景,实现方便集成的大视场高精度流场测量。
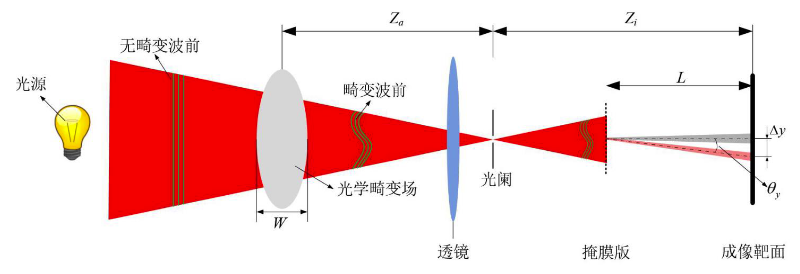
图 1 POS原理光路
如图1所示,具有无畸变波前的光线在穿过光学畸变场之后会出现比较明显的波前畸变。在经过等效镜头组后穿过包含有大量微型通光孔的掩膜版后,变成大量的光束照射到成像靶面上,形成类似图2所示的光斑图像。考虑到普通镜头成像特点,成像靶面上接收的光斑尺寸会比对应通光孔孔径要大,变化量可以通过简单的几何关系粗略计算得到。
|
|
|-|
|图 2 两种掩膜版图案|
图1中掩膜版与成像靶面间的灰色细光束代表了无光学畸变场的光线穿过某个通光孔后形成的光束,相对应的红色细光束是有光学畸变场时光线穿过对应通光孔后形成的,而完整光场将会形成与图2类似的光斑图像。将畸变前后的光斑图像进行比较,可以对光学畸变场实现测量。
为了实现较高的相位分辨率,需要尽可能增大掩模版投影像距$L$,即图1中的掩模版与成像靶面间的距离;同时为了实现较高的空间分辨率,还应尽可能增大掩模版开孔线度。以上两种因素均会放大掩模版开孔的衍射现象,换言之,POS技术的相位分辨率与空间分辨率均受到掩模版衍射物理极限的制约。因此,要需要通过优化设计掩模版开孔方式与光路参数,针对不同的波前测试需求,平衡相位分辨率与空间分辨率,以期实现最优测试效果。
本文旨在通过数值仿真的方式对POS技术中掩模版的衍射现象进行分析,并依照仿真结果对POS光路参数的选择与掩模版加工方式进行针对性优化设计,以降低设计周期与实验成本。
仿真原理
介绍本程序进行衍射仿真计算的理论基础
基尔霍夫公式
|
|
|
|-|-|
|图 3 波阵面示意图|图 4 倾斜因子示意图|
根据惠更斯-菲涅尔原理(Huygens–Fresnel principle),如图3所示的空间中一点$P$的振动等于衍射孔$\Sigma$面上所有的子波源所引发振动的相干叠加,子波源引发振动的振幅与面元$\mathrm{d} s$为正比关系。
$P$点振动的振幅为整个$\Sigma$面上子波源引发振动的叠加,积分表达式为[1]
$$U§= K \iint\limits_{\Sigma} U_{0}\left(x_1, y_{1}\right) \frac{F(\theta,\varphi)}{r} \cos \left({\omega}{t}-\frac{2{\pi}{r}}{\lambda}\right) \mathrm{d} s
\tag{1}$$
上式被称为菲涅尔衍射积分公式(Fresnel Diffractive Integral)。式中,$U_{0}\left(x_1, y_{1}\right)$为$\Sigma$面上的光场分布,$\boldsymbol{r}$是面元$\mathrm{d} s$与场点$P$的距离,$\omega$与$\lambda$分别为光波圆频率与波长;$K$是个特定的比例系数,$F(\theta,\varphi)$为倾斜因子表征由面元引发的次波并非各向同性,但均没有给出具体的定义。
基尔霍夫基于麦克斯韦理论,推导得出比例系数$K = {1}/{ j \lambda}$与倾斜因子$F(\theta,\varphi) = \left(\cos{\varphi} - \cos{\theta}\right)/2$,代入式(1)整理后,得到用于定量求解衍射积分的基尔霍夫衍射公式(Kirchoff’s Diffraction Formula)为[2]
$$U§=\frac{A}{2 j \lambda} \iint\limits_{\Sigma} U_{0}\left(x_1, y_{1}\right) \frac{\exp(\mathrm{jkr})}{r}\left( \cos \varphi -\cos \theta \right) \mathrm{d} s \tag{2}$$
式中,$k = 2\pi/\lambda$, $\theta = {\left \langle \hat{\boldsymbol{n}}, \boldsymbol{l} \right \rangle}$、$\phi ={\left \langle \hat{\boldsymbol{n}}, \boldsymbol{r}\right \rangle}$分别为如图4所示的面元$\mathrm{d} s$法向量$\hat{\boldsymbol{n}}$与照明光波矢$\boldsymbol{l}$、出射光波矢$\boldsymbol{r}$的夹角。
菲涅尔衍射
|
|
|-|
|图 5 两坐标系定义图|
如图5所示建立直角坐标系,用$\left(x_1,y_1\right)$平面描述衍射屏,$\left(x,y\right)$平面描述接收屏,可以将$r$写为[1:1]
$$ r=z_{1}+\frac{\left(x-x_{1}\right){2}+\left(y-y_{1}\right){2}}{2 z_{1}}+\frac{\left[\left(\mathrm{x}-\mathrm{x}{1}\right){2}+\left(y-y_{1}\right){2}\right]^{2}}{8 z{1}^{3}}+\ldots \tag{3}$$
菲涅尔衍射是一种近似情况,当$z_{1}^{3} \gg \frac{1}{4 \lambda}\left[(\mathrm{x}-\mathrm{x}_1){2}+\left(y-y_{1}\right){2}\right]^{2}$时,在傍轴条件下再取倾斜因子$F(\theta,\varphi) = \left(\cos{\varphi} - \cos{\theta}\right)/2\approx1$,(2)式变成
$$U§=\frac{\exp [\mathrm{jkz_1}]}{j z_{1} \lambda} \iint_\limits U_{0}\left(x_{1}, y_{1}\right) \exp \left{\frac{\mathrm{jk}}{2 z_{1}}\left[\left(\mathrm{x}-\mathrm{x}{1}\right){2}+\left(y-y_{1}\right){2}\right]\right} \mathrm{d} x{1} \mathrm{~d} y_{1} \tag{4}$$
也可写为
$$
\begin{aligned}
U§ &=\frac{\exp [\mathrm{jkz_1}]}{j z_{1} \lambda} \exp \left[\frac{\mathrm{jk}}{2 z_{1}}\left(x{2}+y{2}\right)\right] \times \dots
\
&\iint_\limits U_{0}\left(x_{1}, y_{1}\right) \exp \left[\frac{\mathrm{jk}}{2 z_{1}}\left(x_{1}{2}+y_{1}{2}\right)\right] \exp \left[-\mathrm{j} 2 \pi\left(x_{1} \frac{x}{\lambda{z_1}}+y_{1} \frac{y}{\lambda{z_1}}\right)\right] \mathrm{d} x_{1} \mathrm{~d} y_{1}
\end{aligned}
\tag{5}
$$
利用傅立叶变换计算菲涅尔衍射
用$\mathcal{F}$表示傅立叶变换,用$f*g$表示$f$与$g$的卷积,由傅立叶变换的卷积性质,有
$$ \mathcal{F}(f(x,y)*g(x,y)) = \mathcal{F}(f(x,y))\mathcal{F}(g(x,y)) \tag{6}$$
对照式(4),可将菲涅尔衍射的积分式写为
$$
\begin{aligned}
U§ &=\frac{\exp [\mathrm{jkz_1}]}{\mathrm{j z_{1} \lambda}} U_{0}\left(x_{1}, y_{1}\right){ }{*} \exp \left[\frac{j k}{2 z 1}\left(x{2}+y{2}\right)\right]
\
&= \frac{\exp [\mathrm{jkz_1}]}{\mathrm{j z_{1} \lambda}}\mathcal{F}^{-1}\left{ \mathcal{F}\left[U_{0}\left(x_{1}, y_{1}\right){ }\right]{\times} \mathcal{F}\left{\exp \left[\frac{j k}{2 z 1}\left(x{2}+y{2}\right)\right]\right} \right}
\end{aligned}
\tag{7}
$$
计算模型
由于进行衍射传播计算比较消耗计算资源,因此在现阶段对纳入仿真的光路进行简化,仅针对光场通过掩模版这一核心问题进行仿真计算。
本模型将POS光路的入射光场取为叠加了小相位畸变的单色平面波前,经过定焦镜头与等效光阑,最终传播至掩模版。假设镜头组的传递函数可解析得出,抑或是通过镜头组后的光场已经通过仿真得出,则掩模版的照明光波前可以被确认下来。
图 6 衍射系统示意图
对于如图6所示的照明光、掩膜版与成像靶面三者构成的衍射系统,具有考量意义的是三个波前,分别是:掩膜版前侧的照明波前,即入射场$\widetilde{U_0}$;经过掩膜版作用的衍射波前,即透射场$\widetilde{U_t}$;传播到达成像靶面的成像波前,即接收场$\widetilde{U}$。[2:1]整个衍射问题的计算可被分为两个步骤,一是解入射场经过掩膜版作用变为透射场的透射问题,二是解 透射场经过空间传播变为接收场的传播问题。
其中,传播问题可由式(7)解析得出,而透射问题可由屏函数$\widetilde{t}$描述:
$$
\widetilde{t}\left(x_1, y_{1}\right) \triangleq \frac{\widetilde{U_t}{,ref}\left(x_1, y{1}\right)}{\widetilde{U_0}{,ref}\left(x_1, y{1}\right)};
\widetilde{U_t} = \widetilde{U_0}\widetilde{t}
\tag{8}
$$
式(8)意为,对于一个衍射屏可以定义一个屏函数$\widetilde{t}$,透射波前$\widetilde{U_t}$就等于入射波前$\widetilde{U_0}$乘上这个屏函数$\widetilde{t}$。
对于我们关心的掩膜版而言,其屏函数$\widetilde{t}$为
$$
\widetilde{t}(x, y)=\left{\begin{array}{l}
1, \text { 透光部分, } \
0, \text { 遮光部分. }
\end{array}\right.
\tag{9}
$$
代码实现
分析代码结构、演示